由向量到多項式的轉換

一個多項式的 degree 是 n-1 ，因此可以說它具有 n 個點。換言之，在一個有限域中，對於長度為 n 的向量 v 可以視為一個多項式。
一個域其實是一組具有唯一性的元素，而且是與向量 v 具有相同的大小。可以理解為向量 v 代表 y 軸，現在要選擇能代表 x 軸的點。

假設一個例子:
向量 v=0,1,4 並展示如何選擇一個域來定義多項式。
如果 deg(v) = 3，就存在一個2次多項式(degree 為2)。
假設選擇的評估域為 d1 = {1, 0, 3}，用於向量 v 上就可得出這3個點 (1,0)(0,1)(3,4) 及一個多項式: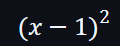

假設選擇的評估域為 d1 = {-1, 0, -3}，用於向量 v 上就可得出這3個點 (-1,0)(0,1)(-3,4) 及一個多項式: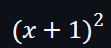

所以相信大家都留意到，可以透過選擇不同的評估域來產生相對應的多項式。
在應用中，所有多項式的域都會是一個有限域，這樣才能被用於計算，否則可能會影響到真實的應用效率。
然而，這個有限域可以由一個具有 n 個單位根的 w 生成。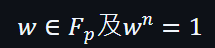

所以可得出以下等式: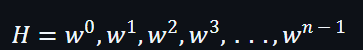

一個有限範圍的評估域對於我們在定義一個合適多項式是十分有用，例如用於零多項式中，
假設零多項式的域是H，所以多項式可以為: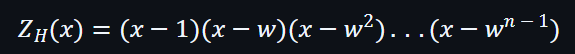

不過當n的值足夠大，就很難計算出評估值，因此可以利用: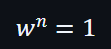

在公式表達上可以重寫為: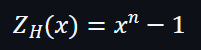

因為: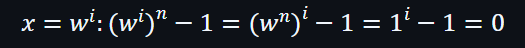

如果域的大小是 n，是電路中口的數量和範圍的大小是 p，而 p 是遠大於 n 。
p 的大小是一個安全參數，所以它的值越大，對協議來說就是越安全。
由於所有 H 的元素都在範圍 F 內和 p 是遠大於 n
而且域是一個範圍 H 的子集: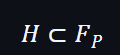

所以是可以知道任何 degree 為 d 的多項式可以用評估形式表示為一組數量為 d+1 的點。
對於 KZG 承諾，其實有多種方法可以將多項式從評估形式轉換為係數形式然後對其進行插值。
接下來會講解如何使用拉格朗日公式來進行實現。
假設大小為 n 的向量 V，在 H 域上可以進行一個插值計算: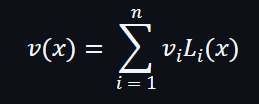

由於: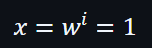

因此: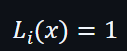

及對於其他插值就會是零，所以加入插值是不會影響到公式的結果。